题目描述

研究完 SARS-CoV-233 病毒的性状后，S 星球开始转而处理因 SARS-CoV-233 而得病的人。

SHO (S-planet Health Organization) 规定，将 SARS-CoV-233 病毒感染的肺炎命名为 COVID-12243。

在 S 星球的这一时期，有众多珂技和卫生会议需要召开。S 星球的会议召开是逐级进行的：

先由 S 星球的联合国在会议中提出若干问题及方法，然后各国的总统将这些精神传达到各省，这样逐级传下去，最后落实到每个人，再汇总起来。

但是，在 Θ 国的各级人民代表大会召开过程中，由于某些乡村的医疗水平不够发达，导致有些村民已经不知不觉地患上了 COVID-12243，然而试剂并不能检验出来。

小 $\omega$ 作为 Θ 国的总统，觉得这件事非常严重。于是，她将亲自下访整条路线，带上高超的试剂，并隔离这些患 COVID-12243 的病人。

形式化地，S 星球的行政区划分为 $n$ 类 (相当于中国的国 - 省 - 市 - 县/区 - 乡等)，从小到大分别称为 $1$ 级行政单位，$2$ 级行政单位，……，$n$ 级行政单位 (Θ 国)。

现在，我们考察一条特定的路线 (即某个乡 $\to \cdots \to$ Θ 国)，其中每一级行政单位中有 $k$ 个人大代表，我们用 $\left( i, j \right)$ 表示 $i$ 级人大代表中的第 $j$ 个。

已知，相邻两级的人大代表会有相互见面的机会，而非相邻两级的人大代表 (即使是同级) 没有相互见面的机会。

(ps: 同级人大代表在开会的时候有某些特殊的措施，导致即使相互见面也不会感染病毒)

对于相邻两级的人大代表，小 $\omega$ 已经调查清楚了：对于 $\forall 1 \leq i \leq n - 1, 1 \leq u, v \leq k$，$\left( i, u \right)$ 和 $\left( i + 1, v \right)$ 是否有相互见面的机会。

现在在 Θ 国需要召开若干次人民代表大会，每次会议的要求如下：

首先，第 $l$ 级行政单位召开人民代表大会，然后第 $l$ 级人大代表和第 $l + 1$ 级人大代表依次见面，然后第 $l + 1$ 级行政单位开始开会，然后再与 $l + 2$ 级人大代表依次见面，……，最终到第 $r$ 级会议开完为止，最后，$r$ 级人大代表需要向小 $\omega$ 汇报消息。

特别地，我们会给定两个集合 $P_l, P_r$，表示 $l$ 级行政单位中，只有 $P_l$ 集合中的人参与整场会议，在 $r$ 级行政单位中，只有 $P_r$ 集合中的人参与整场会议。 而对于 $\forall l < i < r$，$i$ 级行政单位的所有人大代表都必须参加。

但是，目前已知第 $l$ 级的人大代表具有潜在的患 COVID-12243 可能性，而其他人并没有。当两个人见面时，病毒会从下级人大代表传播到上级人大代表。这将导致小 $\omega$ 有一定的几率感染 SARS-CoV-233。

于是，她会选择所有人大代表中的若干个将其隔离，尤其是一些超级传播者。被隔离的人与任何人都不能见面，可以通过特殊的方式传递信息。

但是，将一个人隔离的代价是很大的，所以，小 $\omega$ 希望隔离尽可能少的人，从而确保她不会被感染 (即使会议不能开成功)。

而且，由于某些原因，不同人之间是否有相互见面的机会，是在不断改变的，但始终保持只有相邻两级的人才有相互见面的机会。

注意：在两次不同的会议中，「第 $l$ 级的人大代表具有潜在的患 COVID-12243 可能性」是相互独立的，互不影响。

输入格式

第一行包含三个正整数 $n, k, q$，表示行政单位的种数，每一级人大代表的个数和事件的个数。

接下来 $k \left( n - 1 \right)$ 行，分为 $n - 1$ 段，每段 $k$ 行。

对于第 $i$ ($1 \leq i \leq n - 1$) 段，第 $u$ ($1 \leq u \leq k$) 行包含一个长度为 $k$ 的 $\texttt 0/\texttt 1$ 串，其中第 $v$ ($1 \leq v \leq k$) 个字符为 $\texttt 1$ 表示 $\left( i, u \right)$ 和 $\left( i + 1, v \right)$ 有相互见面的机会，否则表示没有相互见面的机会。

接下来 $q$ 行，每行描述一个事件，格式如下：

1. T i u v 表示 $\left( i, u \right)$ 和 $\left( i + 1, v \right)$ 能否相互见面关系发生改变，即如果原先不能相互见面，则现在能相互见面；如果原先能相互见面，则现在不能相互见面。
2. M l r Pl Pr 表示第 $l \sim r$ 级行政单位开了一次人民代表大会，具体会议的形式见题目描述，其中 $P_l, P_r$ 为 $\texttt 0/\texttt 1$ 串，$P_l$ 的第 $j$ 个字符为 $1$ 当且仅当 $\left( l, j \right)$ 参加这次会议。对于 $r$ 的情况同理。你需要求出被隔离的人数的最小值。

输出格式

对于每次 M 事件，输出一行一个整数，表示需要被隔离的人数的最小值。

样例 1

2 5 13
11000
00100
00100
00100
00011
M 1 2 11111 11111
M 1 2 01110 11011
M 1 2 01010 01110
T 1 2 2
T 1 4 4
M 1 2 11111 11111
M 1 2 01110 11011
M 1 2 01010 01110
T 1 2 2
T 1 4 4
M 1 2 11111 11111
M 1 2 01110 11011
M 1 2 01010 01110

3
0
1
5
2
2
3
0
1

用第一行的点表 $1$ 级人大代表，用第二行的点表示 $2$ 级人大代表，如果两个人大代表能见面，则用一条线段相连，则所得的图形如下：

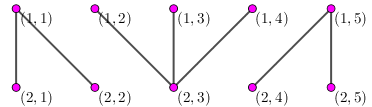
对于第 $1$ 次人民代表大会，所有的人大代表都要参加，于是小 $\omega$ 为了防止自己被感染，需要至少隔离三个人 (隔离用黄圈表示)：

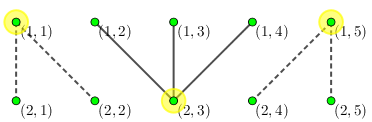
对于第 $2$ 次人民代表大会，只有如下 $7$ 个人大代表需要参加会议，于是这个会议本身就无法成功，小 $\omega$ 不需要隔离任何人：

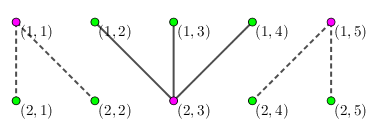
对于第 $3$ 次人民代表大会，只有如下 $5$ 个人大代表需要参加会议，于是为了防止感染小 $\omega$，只需隔离 $\left( 2, 3 \right)$ 即可：

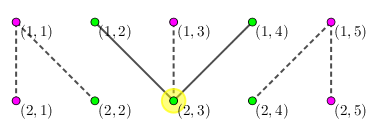
然后，$\left( 1, 2 \right)$ 和 $\left( 2, 2 \right)$ 的见面关系发生改变，$\left( 1, 4 \right)$ 和 $\left( 2, 4 \right)$ 的见面关系发生改变，即新的关系图如下：

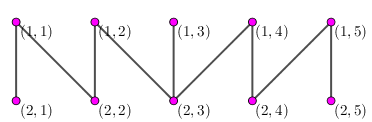
接下来对于第 $4$ 次人民代表大会，所有人大代表都要参加，此时就需要隔离至少 $5$ 个人了：

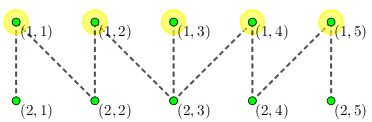
对于第 $5$ 次人民代表大会，还是那时的 $7$ 人参加，不过这回需要隔离 $2$ 个人：

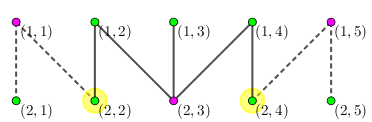
对于第 $6$ 次人民代表大会，有 $5$ 个人参加，这次也隔离 $2$ 个人：

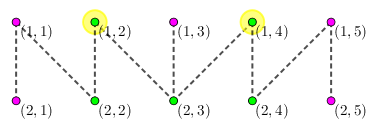
然后，$\left( 1, 2 \right)$ 和 $\left( 2, 2 \right)$，$\left( 1, 4 \right)$ 和 $\left( 2, 4 \right)$ 的见面关系又发生改变，于是她们又无法见面了，从而见面关系图又恢复为最初的形态：

于是接下来的 $3$ 次人民代表大会，所需要隔离的人数和最开始的 $3$ 次相同，为 $3, 0, 1$。

3 2 10
01
10
01
10
M 1 3 10 10
M 1 3 10 01
M 1 3 01 10
M 1 3 01 01
M 1 3 11 11
M 1 2 10 10
M 1 2 10 01
M 1 2 01 10
M 1 2 01 01
M 1 2 11 11

1
0
0
1
2
0
1
1
0
2

注意中间级的所有人大代表都要参加会议。

4 4 1
1000
0000
0000
0000
0100
0000
0101
0000
0000
0000
0000
0001
M 1 4 1111 1111

0

注意病毒只会从下级人大代表传播到上级人大代表，如下图：

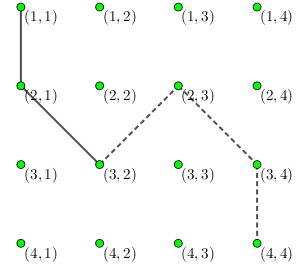
样例 4

见附加文件中的 ex_quarantine4.in 与 ex_quarantine4.out。

数据范围与提示

对于所有的测试点，均满足 $2 \leq n \leq 8192; 1 \leq k \leq 24; 1 \leq q \leq 8192; 1 \leq i \leq n - 1; 1 \leq u, v \leq K; 1 \leq l < r \leq n$。

具体的子任务的数据规模见下表：

子任务	分值	$k$	$n$	$q$	其它性质
1	$3$	$= 1$	$\leq 8192$	$\le 8192$	无
2	$4$	$\leq 2$
3	$4$	$\leq 3$
4	$3$	$\leq 5$
5	$4$	$\leq 7$	$\leq 10$	$\le 10$
6	$3$		$\leq 100$	$\le 100$
7	$3$		$\leq 1000$	$\le 1000$
8	$2$		$\leq 8192$	$\le 8192$
9	$6$	$\leq 9$	$\leq 100$	$\le 100$
10	$5$		$\leq 1000$	$\le 1000$
11	$4$		$\leq 8192$	$\le 8192$	保证对所有会议，有 $l = 1, r = n$
12	$4$				保证所有人大代表的见面关系不改变，即没有 T 事件
13	$3$				无
14	$6$	$\leq 16$	$\leq 100$	$\le 100$
15	$5$		$\leq 1000$	$\le 1000$
16	$4$		$\leq 8192$	$\le 8192$	保证对所有会议，有 $r = l + 1$
17	$4$				保证对所有会议，有 $l = 1, r = n$
18	$4$				保证所有人大代表的见面关系不改变，即没有 T 事件
19	$3$				无
20	$6$	$\leq 24$	$\leq 100$	$\le 100$
21	$5$		$\leq 1000$	$\le 1000$
22	$4$		$\leq 8192$	$\le 8192$	保证对所有会议，有 $r = l + 1$
23	$4$				保证对所有会议，有 $l = 1, r = n$
24	$4$				保证所有人大代表的见面关系不改变，即没有 T 事件
25	$3$				无