题目描述

"分！身！术！" ——小 $P$

平面上有 $n$ 个小 $P$ 的分身。定义一组分身占领的区域为覆盖这组分身的最小凸多边形。小 $P$ 能力有限，每一时刻都会有若干分身消失。但在下一时刻之前，小 $P$ 会使用

"分！身！术！"

使得这些消失的分身重新出现在原来的位置。小 $P$ 想知道，每一时刻分身消失后，剩下的分身占领的区域面积是多少？

输入格式

输入第一行包含两个正整数 $n$ $m$ ，描述初始时分身的个数，和总时刻数。
接下来 $n$ 行，第 $i$ 行有两个整数 $x_i$ , $y_i$ ,描述第 $i$ 个分身的位置。
接下来 $m$ 行，每行的第一个整数 $k$ 表示这一时刻有 $k$ 个分身消失。接下来有 $k$ 个非负整数 $c_1$ , $c_2$ ,... $c_k$ ，用于生成消失的分身的编号。
生成方式如下：
设上一个时刻中，分身占领面积的两倍为 $S$ 。则该时刻消失的分身 $p_1$ , $p_2$ ,... $p_k$ 的编号为 ：

特别的，在第一个时刻，我们认为上一个时刻中，$S = -1$ ,即：第一个时刻消失的分身 $p_1$ , $p_2$ ,... $p_k$ 的编号为：

输出格式

按给出时刻的顺序依次输出 $m$ 行，每行一个整数，表示该时刻剩余分身所占领区域面积的两倍。

样例

6 2
-1 0
-1 -1
0 -1
1 0
0 1
0 0
3 1 3 6
2 0 1

3
2

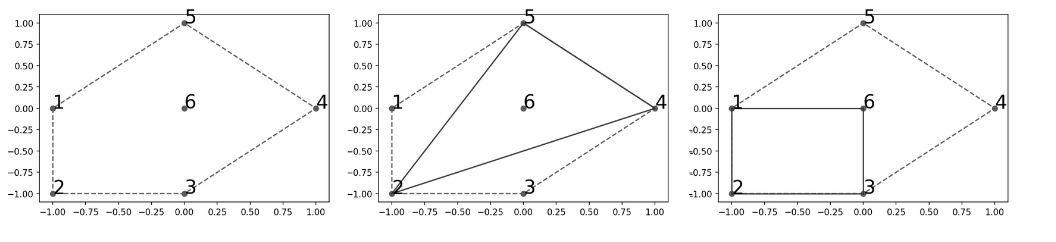
如下图所示：左图表示输入的 $6$ 个分身的位置及它们占领的区域；中图表示第一个时刻的情形，消失的分身编号分别为 $1,3,6,$ 剩余 $3$ 个点占领图中实线内部区域，占据面积的两倍为 $3$ ；右图表示第二个时刻的情形，消失的分身编号分别为:

剩余的 $4$ 个点占领图中实线内部区域。

数据范围与提示

对于所有数据，保证：

• $|x_i| ,|y_i| \leq 10^8$
• 没有两个分身的坐标是完全相同的；
• $k\leq 100$ ；
• 所有时刻的 $k$ 之和不超过 $2\times 10^6$ ；
• $0\leq c_i \leq 2^{31} - 1$
• 初始时，所有的 $n$ 个分身占据区域面积大于 $0$ ；
• 定义所有 $n$ 个分身所占据区域的 顶点集合 为 $S$ , $S\geq 3$ 。在任意时刻中， $S$ 中至少存在两个未消失的分身。

由于 64 位操作系统的指针大小为 8 字节，在 LOJ 上将空间限制扩大为 $768\mathrm{MB}$。