#1840. 「NOI2018」情报中心
「NOI2018」情报中心
题目描述
C 国和 D 国近年来战火纷飞。
最近,C 国成功地渗透进入了 D 国的一个城市。这个城市可以抽象成一张有 个节点,节点之间由 条双向的边连接的无向图,使得任意两个点之间可以互相到达。也就是说,这张无向图实际上是一棵树。
经过侦查,C 国情报部部长 GGB 惊讶地发现,这座看起来不起眼的城市竟然是 D 国的军事中心。因此 GGB 决定在这个城市内设立情报机构。情报专家 TAC 在侦查后,安排了 种设立情报机构的方案。这些方案中,第 种方案是在节点 到节点 的最短路径的所有边上安排情报人员收集情报,这种方案需要花费 元的代价。
但是,由于人手不足,GGB 只能安排上述 种方案中的两种进行实施。同时 TAC 指出,为了让这两个情报机构可以更好的合作,它们收集情报的范围应至少有一条公共的边。为了评估一种方案的性能,GGB 和 TAC 对所有的边进行了勘察,给每一条边制定了一个情报价值 ,表示收集这条边上的情报能够带来 元的收益。注意,情报是唯一的,因此当一条边的情报被两个情报机构收集时,也同样只会有 的收益。
现在,请你帮 GGB 选出两种合法的设立情报机构的方案进行实施,使得这两种方案收集情报的范围至少有一条公共的边,并且在此基础上总收益减去总代价的差最大。
注意,这个值可能是负的,但仍然是合法的。如果无法找到这样的两种方案,请输出 F。
输入格式
从文件 center.in 中读入数据。
本题包含多组测试数据。
输入文件的第一行包含一个整数 ,表示数据组数;
每组数据包含 行:
第 行包含一个整数 ,表示城市的点数;
第 到第 行中,第 行包含三个整数 ,,,表示城市中一条连接节点 和 、情报价值为 的双向边,保证 且 互不相同;
第 行包含一个整数 ,表示 TAC 设立的 种设立情报机构的方案;
第 到 行中,第 行包含三个整数 ,,,表示第 种设立情报机构的方案是在节点 到节点 的最短路径上的所有边上安排情报人员收集情报,并且需要花费 元的代价。
输出格式
输出到文件 center.out 中。
输出文件包含 行;
对于每组数据,输出一行:如果存在合法的方案,则输出一个整数表示最大的总收益减去总代价的差;否则输出 F。
样例
2
5
1 2 1
2 3 3
3 4 2
1 5 8
2
1 4 5
3 5 8
5
1 2 1
2 3 3
3 4 3
1 5 9
2
1 5 5
2 3 8
1
F
这个样例中包含两组数据。这两组数据的城市相同,只是在情报的价值和情报机构的方案上有所不同。城市地图如下:

- 对于第一组数据,方案一中的节点 到节点 的最短路径为 ,方案二中的节点 到节点 的最短路径为 。选择这两种方案需要花费 的代价,并且每一条边的情报都被收集从而得到 的收益,因此总收益减去总代价为 。
- 对于第二组数据,方案一中的节点 到节点 的最短路径为 ,方案二中的节点 到节点 的最短路径为 。这两种方案收集情报的范围没有公共的
边,因此非法,所以这组数据不存在合法方案,应输出
F。
见附加文件中的 center2.in 与 center2.ans。
这个样例只包含一组数据。这一数据中,最优方案为选择第 种和第 种方案。
这组数据的城市地图如下,其中加粗的边表示被情报中心收集情报的边,红色的边表示只被第 种方案的情报中心收集情报的边,蓝色的边表示只被第 种方案的情报中心收集情报的边,紫色的边表示同时被两个情报中心收集情报的边。
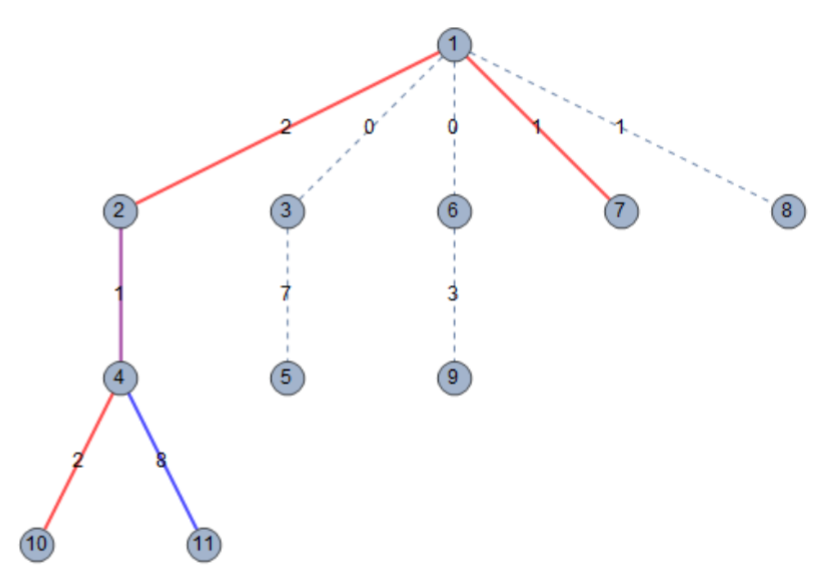
见附加文件中的 center3.in 与 center3.ans。
这个样例和第 个测试点的性质相同。每个测试点的性质见下文的表格。
见附加文件中的 center4.in 与 center4.ans。
这个样例包含了经过特殊构造的 的测试数据,涵盖了测试点中所有出现性质的组合。你可以合理利用这个测试点,对自己的程序进行全面的检查。
这个样例,无疑是善良的出题人无私的馈赠。大量精心构造的 的测试数据,涵盖了测试点中所有出现性质的组合。你可以利用这个测试点,对自己的程序进行全面的检查。足量的数据组数、不大的数据范围和多种多样的数据类型,能让程序中的错误无处遁形。出题人相信,这个美妙的样例,可以给拼搏于 AC 这道题的逐梦之路上的你,提供一个有力的援助。
数据范围与提示
各测试点的数据规模和性质如下表:
| 测试点 | 特殊性质 | |||
|---|---|---|---|---|
| 1 | 保证 | 无 | ||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | 不保证 | |||
| 12 | ||||
| 13 | 保证 | |||
| 14 | ||||
| 15 | 不保证 | |||
| 16 | ||||
| 17 | 保证 | 无 | ||
| 18 | ||||
| 19 | 不保证 | |||
| 20 |
表格中的特殊性质如下:
-
特殊性质 :对于任意 ,保证 到 的最短路径所经过的编号最小的节点不同于 到 的最短路径所经过的编号最小的节点;
-
特殊性质 :对于任意 ,保证 到 的最短路径所经过的编号最小的节点为节点 。
对于所有的数据,,,,。每个测试点中,所有 的和不会超过 ,所有 的和不会超过 。
