#1639. 魔力环
魔力环
题目描述
Shone 喜欢收集黑色与白色的魔力珠。
Shone 希望能够得到一个由 个魔力珠串成的环。不过他对普通的环并不感兴趣,因此他提出了如下的要求:
- Shone 希望在这个环上,恰好有 个黑色的魔力珠与 个白色的魔力珠。
- 由于 Shone 认为黑色魔力珠不应过于密集,因此 Shone 希望这个环上不会出现一段连续的黑色魔力珠,其长度超过 。
在 Shone 的心目中,满足上述要求的环才是美妙的。
不过这样的环可能并不唯一。 Shone 想要知道共有多少种不同的环满足他所提出的要求。然而 Shone 并不喜欢计算,他希望聪明的你能够告诉他答案。
在这里,我们认为两个环是不同的,当且仅当其中一个环仅通过旋转无法得到另一个环。
输入格式
输入包含一行,在这一行中有三个非负整数 ,其意义见题目描述。相邻的两个数用单个空格隔开。
输出格式
输出包含一行一个整数,表示满足要求的环的数量。由于答案可能过大,因此输出答案对 取模后的结果。
样例 1
6 3 2
3
由 个魔力珠串成,满足其中恰好有 个黑色魔力珠与 个白色魔力珠,且不存在长度超过 的连续的黑色魔力珠的不同的环共有 种,如下图所示。
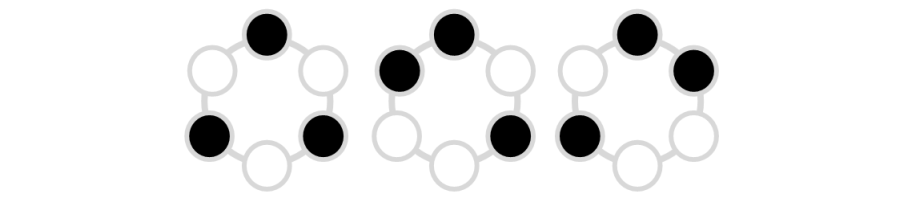
下图所示的环不满足 Shone 提出的要求,因为在这个环中,存在一段连续的黑色魔力珠,长度超过了 。
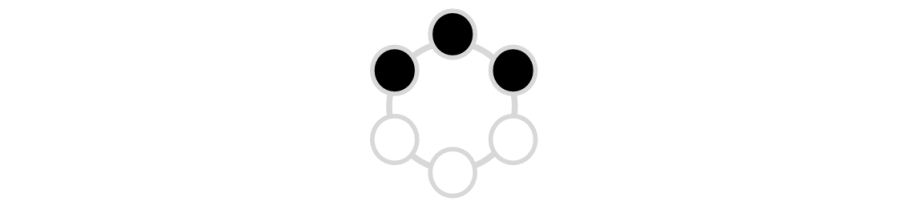
17 8 6
1421
50000 20000 1
683811528
数据范围与提示
所有测试点均满足 $1 \leq n \leq 10^5, 1 \leq k \leq 10^5, 0 \leq m \leq 10^5$ 且 。
单个子任务的具体限制与约定见下表。
| 子任务 | 分值 | 限制与约定 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | 与 的最大公约数不超过 | |
| 7 | 无特殊限制 |
